Estudo científico comprova: partidos brasileiros não são todos iguais
Não é fácil identificar, através do
discurso dos políticos, as diferenças da linha ideológica que os partidos
defendem. Muito menos se formos nos guiar pela nomenclatura dos partidos:
partidos “progressistas” com atuação conservadora, partidos dos “trabalhadores” que atuam magistralmente a favor do
patronato e do capital, e assim por diante. Por isso não é de
admirar que muitas pessoas, levadas pelo senso comum, acreditem que os partidos
brasileiros sejam todos iguais, o que não é e
nunca foi verdade.
Se alguém precisava de uma prova
científica para mudar essa ideia, ela nos foi proporcionada pelo PoliGNU (Grupo
de estudos de software livre da Escola Politécnica da USP) que realizou uma
pesquisa na qual se faz uma comparação numérica sobre a atuação dos distintos
partidos da Câmara de Deputados. (Veja detalhes do estudo AQUI).
Tomando por base 92 votações na
Câmara sobre os mais distintos assuntos, eles compararam como se posiciona em
cada tema os diferentes partidos. O resultado pode ser visto no gráfico abaixo:
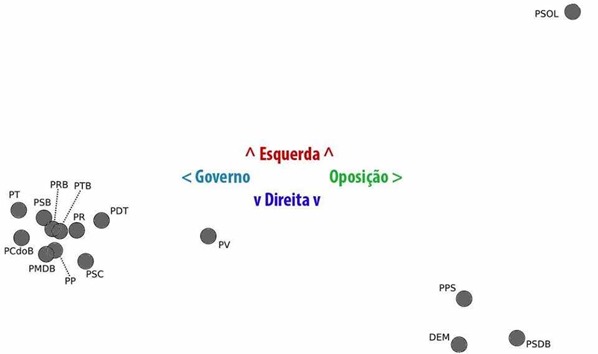
A partir do centro da imagem, que
representa o centro do espectro político-ideológico, temos dois eixos e quatro
direções básicas: direita, esquerda, situação e oposição. O eixo horizontal diz
respeito ao apoio ao governo (situação ou oposição) e o eixo vertical
corresponde à ideologia política (direita ou esquerda) Quanto mais afastado do
centro, mais definido e coerente o partido se apresentou nas votações.
Pelo gráfico, podemos tirar algumas
sentenças: apesar de se dizerem progressistas, os representantes do PT e seus
aliados votaram com uma agenda conservadora (que os posiciona na parte de baixo
da linha horizontal, ou seja, no espetro político da direita; O PCdoB, quem
diria, se posiciona mais à direita do que tradicionais partidos conservadores,
como PR, PRB ou PTB; O PSOL é o partido mais à esquerda do espectro político
nacional, e radicalmente diferente da maioria; O gráfico também ilustra e
derruba uma das maiores falácias da militância petista: apesar de ambos se
posicionarem na oposição, o gráfico mostra que PSOL e PSDB votam completamente
diferentes no Congresso – ou seja, não existe a menor afinidade política entre
esses dois partidos, sendo que a única coisa que têm em comum é a oposição ao
governo (fato devidamente explorado pelos petistas). Por outro lado, são os
próprios deputados petistas que votam com a direita, como ficou demonstrado.
A conclusão mais importante que
podemos tirar desse estudo é que existem sim linhas ideológicas bem definidas
por trás das aparências. E que os partidos mantém uma coerência que pode ser
verificada em suas votações na Câmara. Portanto, mais do que nunca, fica
evidenciado de que os partidos brasileiros não são todos iguais. Cabe aos
eleitores buscarem saber através de informações como votam (e para quem votam)
os deputados, e este estudo é uma ótima ferramenta para se começar a
desmistificar os sensos comuns da política nacional.
Marcadores: politica e sociedade, socialismo e capitalismo
Análise gráfica das votações da câmara dos deputados
Português, Brasil
Update:
O projeto hoje se chama Radar Parlamentar e transformou-se numa ferramenta
interativa que pode ser utilizada em: http://radarparlamentar.polignu.org
Autores:


Autores:
INTRODUÇÃO
Em
nosso primeiro post [1] apresentamos uma comparação numérica entre a atuação dos
partidos na câmara dos deputados baseada nas votações realizadas na câmara. Este
primeiro post rendeu inclusive uma matéria [2] no jornal A Gazeta do Povo, do
Paraná.
Neste novo post
apresentaremos 1) uma nova análise realizada de forma gráfica; 2) uma correção
do cálculo da semelhança, o que resultará em novos valores; e 3) a interpretação
correta para os valores das semelhanças.
ANÁLISE
GRÁFICA
Anteriormente obtivemos
resultados de semelhanças entre partidos dois a dois: podíamos dizer a
semelhança entre PT e PSDB, entre PT e PV, entre PV e PSDB, e assim por diante.
Mas muito mais emocionante do que uma tabela cheia de números é um gráfico que
mostre isso!
Mas tínhamos um grande
problema: como representar todas essas semelhanças em um gráfico ao mesmo tempo?
Note que uma primeira ideia ingênua é fazer com que a semelhança obtida seja
proporcional à distância entre os partidos no gráfico. Mas na verdade fica
impossível desenhar todos os partidos num mesmo plano dessa forma! Se o leitor
não acredita, tente desenhar no papel quatro pontos A, B, C e D obedecendo as
seguintes distâncias: AB=AC=AD=BC=BD=CD=1. Isso não é possível no plano, mas no
espaço com três dimensões teríamos simplesmente o tetraedro regular. Ora, nossos
vetores pertencem a um espaço de 92 dimensões!
Dado
esse problema, um de nós (o Saulo, que não participou do projeto até o primeiro
post) sugeriu o uso da análise de componentes principais, ou PCA [3] na sigla em
inglês.
Trata-se de uma técnica
de análise exploratória de dados, utilizada por exemplo em
data
minning para a extração de
significado de grandes quantidade de dados, em cujas situação a análise manual
seria inviável. Daremos mais detalhes técnicos sobre o PCA na próxima
seção.
E eis que aplicando o
PCA obtivemos o seguinte resultado:
Figura 1 - Resultado gráfico da análise de componentes
principais sobre as votações dos parlamentares na câmara dos deputados
Você pode também obter o gráfico em formato SVG clicando aqui
(ou no anexo do post).
Atenção, os dados de
entrada para essa análise foram as mesmas 92 votações utilizadas no último
post.
Nesta
análise a intenção era colocar todos os partidos, mas deixamos alguns de fora,
pois são pequenos partidos (PRTB, PRP, PSL, e PHS com 1 deputado, e PMN, com 2
[4]) que estiveram totalmente ausentes em pelo menos alguma votação. Essa
característica causa dificuldades matemáticas em nossa análise, e por isso eles
foram excluídos.
COMO
ISTO FOI FEITO // Álgebra linear!
A entrada do algoritmo
PCA é um conjunto de vetores, que no nosso caso são os vetores de votações (cada
partido possui um vetor, em que cada posição representa uma votação e cada valor
representa a posição média do partido em relação à votação daquela
posição).
O que
algoritmo faz na verdade é uma mudança de base, resultando em uma base
ortogonal, de forma que os vetores resultantes apresentem a seguinte
propriedade: o desvio padrão entre os valores da primeira coordenada (na nova
base) dos diversos vetores é máximo. O desvio padrão entre os valores da segunda
coordenada é máximo desde que o segundo vetor da base seja ortogonal ao
primeiro. Ou seja, se tomarmos um conjunto A formado pelos primeiros elementos
de cada vetor da saída do PCA, e um conjunto B formado pelos segundos elementos
de cada vetor da saída do PCA, teremos que o desvio padrão entre os elementos de
A é maior que o desvio padrão dos elementos de B. Portanto, os vetores da nova
base, chamados "componentes principais" são ordenados de forma que o primeiro
deles é na direção da maior dispersão dos dados, o segundo segue a maior
dispersão ortogonal ao primeiro e assim por
diante.
Isso na prática quer
dizer que as diferenças mais significativas entre os partidos foram acumuladas
nas primeiras dimensões! Com isso, utilizamos as duas primeiras dimensões do
vetor de cada partido para definir sua posição em um plano bi-dimensional (nosso
gráfico).
Assim, é como se nosso
gráfico fosse uma espécie de sombra bi-dimensional de um conjunto de dados
multi-dimensionais (no nosso caso 92 dimensões). No entanto não é uma sombra
qualquer, mas sim a sombra projetada de um ângulo que nos mostra muito bem o que
queremos enxergar. De forma análoga, pense na sombra de uma pessoa: ao meio-dia
a sombra da pessoa é aproximadamente um círculo em baixo dela, o que é uma má
aproximação (pois estamos projetando segundo as direções x e y, sendo que a
informação mais significativa está na altura, no eixo z), mas em outros horários
já teremos sombras que revelam a forma humana.
INTERPRETAÇÃO DA
ANÁLISE GRÁFICA // Política!
A primeira coisa
importante a se dizer, é que a posição de cada partido foi totalmente definida
pela análise PCA com base na comparação mútua entre as votações de todos os
partidos.
Os significados dos
eixos obtidos podem ser por nós atribuídos tendo em vista o resultado. Ou seja,
após uma inspeção manual é nossa interpretação que diz
que:
-
O eixo horizontal está relacionado ao apoio ao governo, indo da situação (lado esquerdo) para a oposição (lado direito).
-
O eixo vertical está relacionado à ideologia, indo da esquerda (cima) para a direita (baixo).
Outro fato importante
vindo da análise PCA é que a primeira dimensão é a mais representativa. No nosso
caso, esta “primeira dimensão” corresponde ao nosso eixo horizontal, o que quer
dizer que a semelhança entre os partidos, i.e. a maneira de cada partido votar,
é definida mais em função do apoio que cada partido dá ao governo do que por
suas próprias ideologias. Isso pode ser enxergado através da observação de que o
espectro de apoio ao governo (largura do gráfico) é bem mais amplo do que o
espectro "ideológico" (altura do gráfico). Mais especificamente, a primeira
componente explica 73% da variância, e a segunda explica
9,6%.
Alguns pontos
notáveis:
-
O PT está na “extrema situação”, o que é o resultado mais sensato possível, já que é o partido do governo; mas note que na nossa modelagem matemática nada induzia a isso, logo este resultado foi realmente uma demonstração de incrível poder da análise PCA!
-
Se retirarmos o PSOL, o PT se mantém como o partido mais ideologicamente à esquerda (embora dentro de um espectro ideológico bem mais reduzido).
-
O PSOL se caracteriza como um partido radicalmente diferente de todos os demais.
-
O PV também aparenta ser um caso atípico, porém com posições mais “centralizadas”, mas se afastando o suficiente para justificar a candidatura própria em oposição ao PT.
-
Existem poucos partidos realmente de oposição atuando na câmara. O maior bloco de oposição é o conjunto PSDB, DEM e PPS.
-
Dentro do bloco do governo (Figura 2), o PDT é o partido mais opositor, embora seja (ou “por ser”?) o partido de origem da presidenta!
-
Dentro do bloco do governo, notamos que PP, PSC e PMDB estão mais ideologicamente à direita. Isto pode representar uma tentativa de manter uma mínima identidade ideológica, uma vez condicionado o apoio de forma geral ao governo.
Figura 2 - Mesmo gráfico da análise PCA focada no "bloco
próximo ao governo"
NOVO RESULTADO NA
ANÁLISE NUMÉRICA
Na
análise anterior a posição de um partido sobre uma votação era representado com
um número de 0 a 1, em que 0 representava “todos os deputados do partido votaram
não”, enquanto que 1 representava “todos os deputados do partido votaram sim” (o
valor 0,5 poderia significar a abstenção dos parlamentares ou a divisão de
opiniões dos parlamentares do partido).
No entanto, ao rever os
métodos observamos que utilizar uma faixa de -1 a 1 resultaria em resultados
mais justos do que utilizar a faixa de 0 a 1, no caso de a medida de semelhança
ser o produto escalar. No último post, o leitor Danilo sugeriu nos comentários
que investigássemos também a medida linear de distância, e vamos aproveitar para
discorrer sobre a diferença entre estas duas medidas através do exemplo a
seguir:
Sejam quatro partidos A, B,
C e D, e três proposições x, y e z. O partido A foi unânime nas três votações,
dizendo sim para x e não para y e z, o que representamos assim com as escalas 0
a 1 (sem linha) e -1 a 1 (com linha):
a = (1,0,0); a'=
(1,-1,-1)
Analogamente, os outros
partidos votaram como segue:
b = (0,1,0); b'=
(-1,1,-1)
c = (0,0,0).
c'=(-1,-1,-1)
d = (0,1,1);
d'=(-1,1,1)
Comparando com o partido A, é
nítido que o partido D é o mais ortogonal: votou o contrário do A em todas as
proposições. Gostaríamos que a semelhança entre eles fosse zero. Já o partido C
votou como A em duas proposições e diferiu apenas em uma, e B diferiu de A em
duas. Observe as semelhanças abaixo (calculadas com o produto escalar) e note
como a escala entre 0 e 1 não reflete estas observações. Ao lado, mostramos
também a distância em linha reta entre os dois vetores, que traz mais
informação: por exemplo a distância maior está entre os partidos A e D, que
discordam em tudo:
sem(a,b) = 0 % dist(a,b) =
1,41
sem(a,c) = 0 % dist(a,c) =
1
sem(a,d) = 0 % dist(a,d) =
1,73
Já na escala entre
-1 e 1 temos:
sem(a',b') = 33%
dist(a',b') = 2*1,41 = 2,82
sem(a',c') = 67%
dist(a',c') = 2*1 = 2,00
sem(a',d') = 0% dist(a',d')
= 2*1,73 = 3,46
A medida de distância
simplesmente foi multiplicada por dois. Já a semelhança tal como medida pelo
produto escalar nos trouxe informações interessantes: a semelhança entre A e D
resultou zero, o que nos diz imediatamente que os dois discordam sempre. É fácil
ver que para ter 100% dois partidos teriam que concordar sempre, e a semelhança
de A com B e C mostra valores graduais. Concluímos que o valor obtido com o
produto escalar apresenta uma interpretação mais direta do que a distância
linear, em termos de porcentagens. Essa interpretação será explorada com mais
detalhes na próxima seção.
Contudo, uma observação
interessante é que o resultado da análise gráfica (resultado da PCA) é o mesmo
tanto para os antigos vetores de votações, quanto para os novos vetores agora
apresentados. Isso acontece justamente porque na PCA estamos tratando das
distâncias (e posições relativas) entre os partidos, e não propriamente dos
ângulos. Para a PCA, a posição da origem (o zero) não faz diferença (pois ela é
reposicionada na média no início da análise, afim de colocar em evidência as
diferenças). O resultado visual que temos no gráfico reflete as distâncias
lineares entre os partidos, e nada tem a ver com os
ângulos.
Após
efetuar tal alteração, obtivemos uma nova lista de semelhança entre os partidos.
Confira a nova lista de semelhança entre os partidos clicando
aqui.
O efeito observado foi
de que maneira geral os partidos se aproximaram, ou seja, eles
todos são mais parecidos ainda do que supunha a análise anterior. No
entanto os “agrupamentos de partidos” se mantiveram os mesmos,
como por exemplo: o PSDB continua sendo mais próximo ao DEM do que ao
PT.
INTERPRETAÇÃO
DOS VALORES NUMÉRICOS DAS SEMELHANÇAS
Um problema da análise
anterior, é que o valor obtido de semelhança (aquela porcentagem) não tinha uma
interpretação direta. Por exemplo, dada a semelhança de 43% entre PT e PSDB, o
que significa esse 43%?
Alguém poderia ser
tentado a dizer que o PSDB apoiou o PT em 43% das propostas analisadas. Mas na
verdade não é bem isso... o resultado era apenas uma quantificação para dar a
ideia desse nível de apoio, mas a interpretação não era tão
direta.
Com o novo método
apresentado na seção anterior para o cálculo da semelhança, formulamos uma
interpretação mais concreta para os números.
A interpretação nem sempre é
direta porque os partidos têm nuances nas votações, e nem sempre votam "em
bloco" (diremos que o partido vota "em bloco" quando todos do partido votam
igual em uma votação). Contudo é possível explicar com palavras simples em
alguns casos particulares.
O caso particular mais simples
é o caso em que os dois partidos, A e B, votam sempre em bloco, em todas as
votações. Neste caso, o valor 43% é a porcentagem de votações em que os dois
partidos concordaram, e o complemento, 57%, é a porcentagem em que
discordaram.
Um caso particular menos
restritivo é o caso em que um dos partidos, por exemplo o partido A, sempre vota
em bloco, mas o partido B pode apresentar divisões internas em algumas questões.
Vamos supor que o partido B tenha 4 parlamentares, e que em certo período foram
feitas 25 votações. Neste caso, houveram 100 votos do partido B, 4 para cada uma
das 25 votações. O número 43% nos diz então que 43 destes 100 votos foram
concordantes com a opinião do partido A (que tem sempre uma opinião única nas
votações), e os demais votos foram discordantes.
No caso geral em que também o
partido A apresenta divisões internas, uma interpretação em palavras do valor
43%, que seja ao mesmo tempo correta e completa, começa a ficar mais complicada.
No exemplo acima, como há 25 votações, cada uma delas corresponde a 4% do total.
Para as votações mais simples de analisar, em que os dois partidos, A e B,
votaram em bloco, ou eles concordaram plenamente ou discordaram plenamente. Se
concordaram soma-se 4% na semelhança entre os dois, e se discordaram não se soma
nada. Para uma votação em que, por exemplo, os 4 parlamentares de B se
dividiram, apenas 3 concordando com A enquanto que o quarto discordou, somamos
apenas 3%. Para as votações em que ambos os partidos se dividiram, a porcentagem
a somar seria:
4% * (%Asim * %Bsim + %Anão
* %Bnão)
Onde o 4% = (100%) / (Número
de votações) representa a semelhança máxima que pode ser advinda daquela
votação; se houvessem 100 votações cada votação "valeria" apenas 1%. A fórmula
acima funciona, é claro, também nos casos particulares em que há votações em
bloco.
Exemplo: Em uma dada
votação os votos se distribuíram como segue:
A votou sim sim sim sim não -> representado na
álgebra por (1+1+1+1-1)/5 = 0,6
B votou não sim não não
-> representado na álgebra por (-1+1-1-1)/4 = -0,5
4% * (%Asim * %Bsim + %Anão
* %Bnão) = 4% * (.8*.25 + .2*.75) = 4% * (.2 +.15) =1,4%
No produto escalar, esta
coordenada (votação) irá contribuir com 0,6*-0,5 = -0,3. Como o mapeamento é 0%
para -1 e 100% para +1, a contribuição seria 35% do máximo que se pode atingir,
o que mostra que os dois jeitos de pensar (com a álgebra ou com as porcentagens)
são equivalentes.
PRÓXIMOS
PASSOS
-
Questionar a câmara porque os web services retornaram apenas 27 das 693 proposições votadas em 2011. A totalidade desses dados seria importante para obter um resultado mais preciso!
-
Obter dados de anos anteriores, o que possibilitará uma “análise temporal”. Idealmente esses dados devem ser desde 1988.
-
Obter dados sobre os partidos com ministérios em cada ano, assim podemos relacionar o apoio ao governo nas votações da câmara com a ceção de ministérios para esses partidos.
-
Analisar que votações contribuem mais para os primeiros componentes principais, afim de descobrir (automatica- e matemagicamente) quais são as questões "polêmicas", que causam mais divergências na câmara.
-
Avaliar as dispersões internas entre os partidos.
-
Incluir o tamanho dos partidos na representação gráfica.
REFERÊNCIAS
[1] Primeiro post sobre
o camaraws: http://projeto/camaraws/análise-automatizada-da-semelhança-entre-os-partidos-políticos
[2] Matéria no jornal
Gazeta do Povo sobre o camaraws: http://www.gazetadopovo.com.br/vidapublica/conteudo.phtml?tl=1&id=1217527&tit=Fidelidade-a-toda-prova
[3] Análise de
componentes principais (PCA): http://en.wikipedia.org/wiki/Principal_component_analysis
[4] Tamanho das bancas
dos partidos na câmara: http://www2.camara.gov.br/deputados/liderancas-e-bancadas
Projeto:

21 comments
Muito bacana!
Enviado por Anônimo em ter, 14/02/2012 - 16:19Situação versus Oposição
Enviado por Anônimo em ter, 14/02/2012 - 16:20Leonardo,Novamente parabéns.
Enviado por Anônimo em ter, 14/02/2012 - 18:59Nossa, apesar de não entender
Enviado por Anônimo em ter, 14/02/2012 - 21:15Muito interessante, parabéns!
Enviado por Anônimo em ter, 14/02/2012 - 22:34Eu ia sugerir exatamente o que vocês planejaram pros próximos passos: "Incluir o tamanho dos partidos na representação gráfica". A maneira mais direta que vejo é a área do círculo sendo proporcional ao tamanho do partido.
Uma outra coisa bastante interessante seria usar dados de anos anteriores, como vocês planejam, e criar um gráfico "animado", como esse do Google (http://code.google.com/apis/chart/interactive/docs/gallery/motionchart.html#Example), e ver como os partidos se movimentam com o tempo (os que mudam de ideologia, mudam de situação pra oposição, mudam de grupos, etc).
Eixo ideológico
Enviado por Anônimo em qua, 15/02/2012 - 00:09Respondendo às perguntas
Enviado por Anônimo em qua, 15/02/2012 - 09:23
Enviado por leofl em qua, 15/02/2012 - 09:36@leofl acho que essa parte
Enviado por Anônimo em qua, 15/02/2012 - 22:08s/a variância restante/a
Enviado por Anônimo em qua, 15/02/2012 - 22:15Fidelidade partidária
Enviado por Anônimo em qua, 15/02/2012 - 10:05Olá Jorge,
Enviado por leofl em qua, 15/02/2012 - 14:57de fato, até já no deram também essa ideia de fazer "manchas de deputados" em vez de circunferências de partidos. Espero que cheguemos lá!
Mas quanto ao tamanho do partido ser representado, acredito que já será para mais em breve.
Sugestão nas melhorias
Enviado por Anônimo em qui, 16/02/2012 - 20:24Espero que cheguemos lá!
Enviado por leofl em ter, 21/02/2012 - 23:04Parabéns
Enviado por Anônimo em sex, 17/02/2012 - 10:44Olá Max,
Enviado por leofl em ter, 21/02/2012 - 23:12em primeiro lugar, a sacada da ACP devemos ao Saulo! :)
O "total da variância explicada para os dois eixos" está no post. É de 73% para o eixo horizontal e 9,6% para o eixo vertical.
> "foram mais de 600 votações, mas nem todas foram nominais, o que não entra no sistema da câmara, das nominais não foram 100"
desculpa, não entendi sua frase... só sei que das mais de 600 proposição, só conseguimos analisar 27 proposições (mais de 90 votações)
Como assim "analisando por redes"? num saquei x)
Quanto ao gráfico animado, é o que queremos fazer! =D
Partido duplicado
Enviado por Anônimo em sex, 17/02/2012 - 16:43Achei a origem desta
Enviado por Anônimo em sex, 17/02/2012 - 16:53Nossa, muito obrigado Marcos!
Enviado por leofl em ter, 21/02/2012 - 23:07Legal, esta é a ideia toda do software livre, permitir que a comunidade encontre erros e participe do desenvolvimento =)
Ótimo trabalho, mas o povo não entende nada.
Enviado por Anônimo em sex, 20/07/2012 - 10:54Pena que quem entende tudo isso, no universo "povo brasileiro", são duas minorias desse país varonil: os menos de 1% que têm acesso à educação superior de qualidade (ainda assim me questiono se realmente a totalidade do 1% entende esse trabalho), mas que são totalmente deixados de lado pelo governo; e os tradicionais grupos ricos que realmente dão as cartas nesse país (situação da qual a maioria massacrante daquele "povo brasileiro" se convence, erroneamente, de que não há como reverter esse quadro).
Mas para graduandos, graduados e pós-graduados, esse trabalho é muito interessante e de leitura obrigatória, independente das opiniões ideológicas. Vamos ver se a galera entende. Poderia ser uma mudança de rumo desse país.
Valeu!
Mudanças
Enviado por diraol em ter, 07/08/2012 - 02:10obrigado pelos elogios!
Acho que parte desse nosso trabalho é a crença na mudança de paradigmas, quem sabe juntar o "saber popular" com o "saber científico" e com o "saber digital", e fazer sair dai algo de diferente. Levar a cultura hacker além do submundo da tecnologia. Não que isso seja fácil, mas se não começarmos nunca chegaremos lá né?!
Abraços!